INQUIRY ACTIVITY SUMMARY
As we know there are several right triangles. However, there are three examples of right triangles that we call "Special Right Triangles." These triangles are the 30, 45, and 60 degrees triangles, which have some special features as shown in the pictures below.
http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/6d31e6a7-f698-4f44-b2d2-953443b2e5bd.png *(edited by me)
30 degrees
First we labeled the rules of this special right triangle. Them being the hypotenuse is 2x, vertical value = x and horizontal value = x√3.
The next step to this triangle was to find a way to which we can make the hypotenuse equal 1. The way to do this is to divide 2x by itself making it equal 1. As we know, whenever a change is done to a side, the same change must be done to the other sides. Due to this, we divide x and y by 2x leaving us with horizontal value = √3 / 2 and vertical value = 1 / 2
Now you just equal the hypotenuse to r, horizontal value to x and vertical value to y. r = 1, x = √3 / 2, and y = 1 / 2.
Then you draw a plane on the triangle so that the triangle lies on quadrant I
Finally you label the three points on the triangle. The points for this triangle should be (0,0), (√3 / 2, 0), (√3 / 2, 1 / 2)
45 Degrees
First we labeled the rules of this special right triangle. Them being
the hypotenuse is x√2, vertical value being x and horizontal value also being x.
The next step to this triangle is to find a way to which we can make
the hypotenuse equal 1. The way to do this is to divide x√2 by itself
making it equal 1. As we know, whenever a change is done to a side, the
same change must be done to the other sides. Due to this, we divide the horizontal and vertical values by x√2 leaving us with horizontal value = √2 / 2 and vertical value
= √2 / 2.
Now you just equal the hypotenuse to r, horizontal value to x and vertical value to y. r = 1, x = √2 / 2, and y = √2 / 2.
Then you draw a plane on the triangle so that the triangle lies on quadrant I
In the end, you label the three points on the triangle. The points for this triangle should be (0,0), (√2 / 2, 0), (√2 / 2, √2 / 2)
60 Degree
First we labeled the rules of this special right triangle. Them being
the hypotenuse is 2x, vertical value = x√3 and horizontal value = x.
The next step to this triangle was to find a way to which we can make
the hypotenuse equal 1. The way to do this is to divide 2x by itself
making it equal 1. As we know, whenever a change is done to a side, the
same change must be done to the other sides. Due to this, we divide x
and y by 2x leaving us with horizontal value = 1 / 2 and vertical value
= √3 / 2.
Now you just equal the hypotenuse to r, horizontal value to x and vertical value to y. r = 1, x = 1 / 2, and y =√3 / 2.
Then you draw a plane on the triangle so that the triangle lies on quadrant I.
Finally you label the three points on the triangle. The points for this triangle should be (0,0), (1 / 2, 0), (1 / 2, √3 / 2)
How does this activity help you to derive the Unit Circle?
This activity helped me not only to find the points that we will be using in the unit circle later in the unit but also to visualize where those points came from. Now these points are not just random numbers that were thrown at me to memorize. I understand the background of the numbers, and how they relate to the angles. This activity will also help when I have to use the trig functions because I will know which numbers I have to use for each one of the functions. In conclusion, this activity helped me understand where the unit circle's values come from and how I can use them later in the unit.
Quadrants and Signs
Something that is very interesting about these triangles is that once you found the I quadrant you can figure out what the other sides are because the values will be the same the values will just change signs. First,you base yourself on the reference angle to measure the 30, 45, and 60 degrees.Once you do this you can start assigning the numbers. On Quadrant II , the numbers will be the same. The only thing that will change will be the sign on the x value. On Quadrant III, you still base yourself on the reference angles, then the change on this quadrant will be that both the x and y value will be negative. Finally, in Quadrant IV they only change that has to be done is that the y value will be the only one negative. x will stay positive.
INQUIRY ACTIVITY REFLECTION
The coolest thing I learned from this activity was…how everything that we learned in the unit falls together through something like this (unit circle). I also found very interesting how past courses such as geometry and algebra II had such a great influence on something like this where you relate angles with circles and triangles.
This activity will help me in this unit because… it will help me not only know the values that i will be needing when I need to use the unit circle but to understand where it comes from. So that in case I ever forget how all these numbers came to be and I forget the values I know where I can get these values
Something I never realized before about special right triangles and the unit circle is… how the both of them compliment each other so much. I never thought that through triangles I'd understand how a circle works and through that we can find different values along with the trig functions.

.JPG)
.JPG)
.JPG)



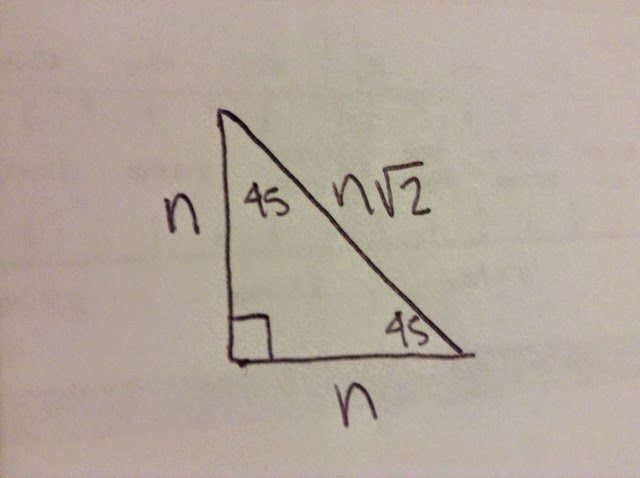


















.JPG)