First we have the triangle as shown above.
Then we divide the triangle in half making one of the 60 degree angles become two 30 degree angles. By doing this we also create two 90 degree angles. Now we have to find the missing side being the dotted line. we can do this with the pythagorean theorem. With the bottom being 1/2 and the side being 1. The answer should be y = rad3 / 2. Then we multiply all the values of the triangle by two so that we don't have any fractions.
How can we derive the 45-45-90 triangle from an square with a side length of 1?
First you draw the square and label each one of the sides one.
Then you make a diagonal dividing the square into two triangles. You may notice that these are the two triangles are the triangles that you're looking for (45, 45, 90)
Then you use the pythagorean theorem to find the length of r. this resulting to be rad2.
Then when you get that you multiply it by n so that you get the derivation of the 45 - 45 - 90 triangle, as shown below
Something I never noticed before about special right triangles is…
That they are derived from another shape and the angles come from there.
Being able to derive these patterns myself aids in my learning because…
now I where the formulas and the angles come form. if one day I don't remember how the concept works I can always come back here and know the basics of the special right triangles.
.JPG)
.JPG)
.JPG)



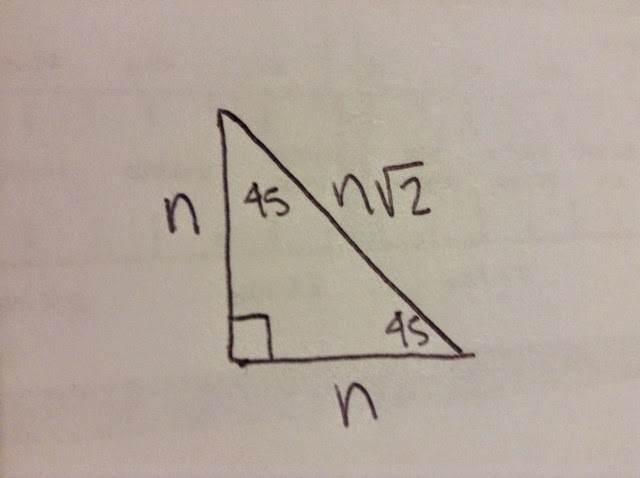
No comments:
Post a Comment